Náročnější výpočty
To, co ses doteď naučil, byl absolutní základ. Je šance, že ti to na střední škole bude stačit, ale jestli tě zajímají další výpočty \( \mathrm{pH} \), tak mrkni na ukázku níže.
V těchto řádcích se dozvíš, jak vypočítat složitější příklady na pH. Konkrétně se bude jednat o soli, které hydrolyzují, a pufry. Že i u nich se pH dá celkem jednoduše spočítat a hlavně jak, zjistíš tady. Mimo to se můžeš i podívat na stupnici pH z látek z běžného života.
Výpočet pH solí a pufrů
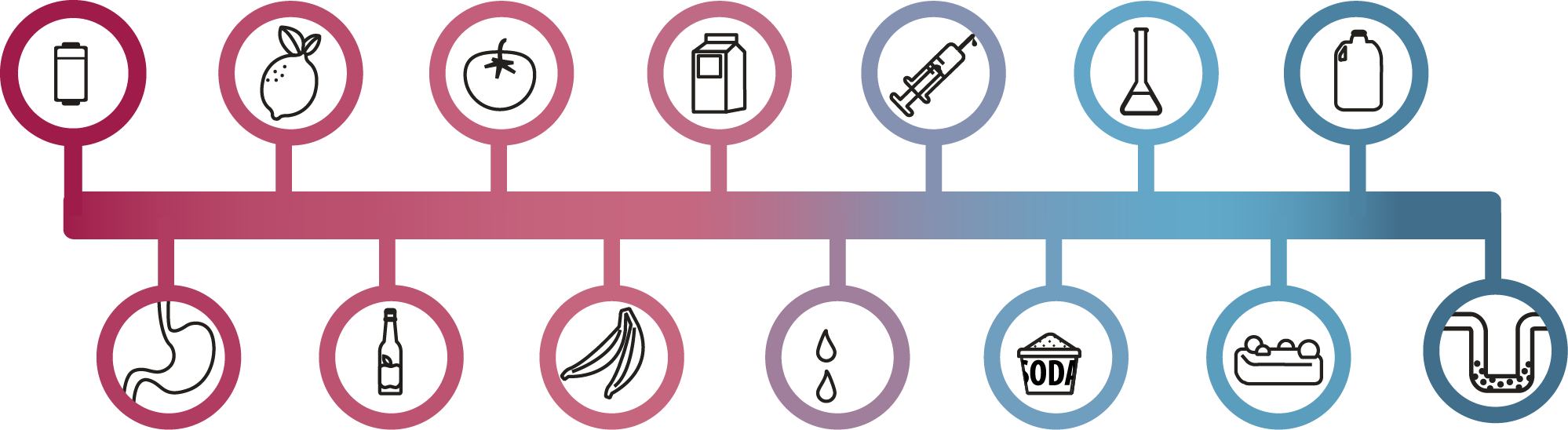
Dříve než se podíváme na tyto výpočty se můžeš pro zajímavost podívat ještě i na tento obrázek, který ti ukazuje stupnici pH a jednotlivé příklady ze života:
Soli, které pochází ze slabé kyseliny nebo slabé zásady, ve vodném roztoku hydrolyzují.
Ukážu ti to na chloridu amonném, což je sůl silné kyseliny a slabé zásady.
\( \textrm{NH}_4\textrm{Cl} → \textrm{NH}_4^+ + \textrm{Cl}^− \)
\( \textrm{NH}_4^+ + \textrm{H}_2\textrm{O} ⇄ \textrm{NH}_3 + \textrm{H}_3\textrm{O}^+ \)
Amonný kation předá část \( H^{+} \) vodě, vznikne tedy amoniak. pH roztoku je kvůli vzniklým iontům \( H_3O^{+} \) kyselé. Vzniká rovnováha mezi amonným kationtem a amoniakem, kterou číselně popisuje rovnovážná konstanta \( K_{A} \). pH se spočítá dle následující rovnice:
\( \textrm{pH} = 7 − \frac{1}{2} \textrm{p}K_\textrm{A} − \frac{1}{2} \textrm{log}\ c (\textrm{NH}_4\textrm{Cl}) \)
Pro soli slabých kyselin platí něco podobného, jen si slabá kyselina od vody „půjčuje“ \( H^{+} \), z molekuly vody zbude \( OH^{-} \), proto jsou tyto roztoky zásadité. Ukážu ti to na kyanidu draselném.
\( \textrm{KCN} → \textrm{CN}^− + \textrm{K}^+ \)
\( \textrm{CN}^− + \textrm{H}_2\textrm{O} ⇄ \textrm{HCN} + \textrm{OH}^− \)
Platí vztah:
\( \textrm{pH} = 7 + \frac{1}{2} \textrm{p}K_\textrm{A} + \frac{1}{2} \textrm{log}\ c (\textrm{KCN}) \)
Dále ti něco povím o pH pufrů. Pro kyselé pH se používá slabá kyselina a její sůl se silnou zásadou (např. kyselina octová a octan sodný). Pro bazické pH se používá slabá zásada a její sůl se silnou kyselinou (např. amoniak a chlorid amonný). Pro výpočty pH pufrů se používáHendersonova-Hasselbalchova rovnice:
Pro kyselý pufr:
\( \textrm{pH} = \textrm{p}K_\textrm{A} − \textrm{log} \frac{c (\textrm{HA})}{c (\textrm{BA})} \)
Pro zásaditý pufr:
\( \textrm{pOH} = \textrm{p}K_\textrm{B} − \textrm{log} \frac{c (\textrm{B})}{c (\textrm{BA})} → \textrm{pH} = 14\ −\ \textrm{p}K_\textrm{B} + \textrm{log} \frac{c (\textrm{B})}{c (\textrm{BA})} \)
HA je kyselina, B je báze a BA je sůl.
Nejúčinnější je pufr, pokud je koncentrace kyseliny/báze a soli stejná. Tehdy člen s logaritmem podílu koncentrací je roven jedné. Jelikož je logaritmus jedničky roven nule, pH se u kyselého pufru rovná \( pK_{A} \) a pOH se u zásaditého pufru rovná \( pK_{B} \).